机器人中的速度概念
在机器人领域,运动可以说是一个永不过时的话题,因为我们制造机器人最主要的目的就是替代人类从事体力劳动,这当然离不开运动了。而谈到运动也离不开一个基本概念 —— 速度。要弄明白运动学和动力学,速度可是绕不过去的重要概念,这可能也是挡在初学者面前的第一只拦路虎。在不同的机器人教科书中甚至采用了不同的表示方法,不同的速度概念之间也少有人去解释它们的关系和转换方法。
点的速度
如果我们将机器人简化成由一些质点组成(有些情况确实可以这么做),那么事情就简单了。因为如果一个点 p 的位置向量 $\textbf{p}$ 可以用三维坐标$ (x,y,z)$表示的话,那么它的速度就是位置的坐标分量对时间 t 的导数,见式 (1)。这个定义简单粗暴,我想不出更简洁的方式了,那我们就采用这个定义吧。
$$\frac{d\textbf{p}}{dt}=\left(\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}\right)\tag{1} $$
*为了简洁,以后我们有时也会将$\frac{d\textbf{p}}{dt}$记为 $\dot{\textbf{p}}$或者 $v_{p}$。
刚体的姿态——大麻烦
可是点毕竟有些过于简单了,更接近实际的假设是将机器人视为由一些刚体组成。在推导速度之前,我们先要给出刚体的位置等状态的描述方法。对于刚体,只描述它的位置是不够的,我们还要描述它的姿态(或者叫朝向)。描述刚体的位置并不难,只要我们选择刚体上的一点,然后用这个点的坐标就能表示刚体的位置了。这个点该如何选择取决于你要解决的问题,怎么方便怎么来,比如你想建立动力学模型,那么最好选择质心这个点。
如果平移运动是个听话的乖宝宝,那旋转运动就是让人捉摸不透的老油条。其原因就在于平移变换是一个欧式空间,而旋转变换则是一个非欧空间(更确切的说是一个李群,等到后面我会进一步介绍这具体是什么意思,我们暂时不管这个)。我们一下子从初中生难度进入了研究生难度,这个跳跃让很多初学者都不习惯。
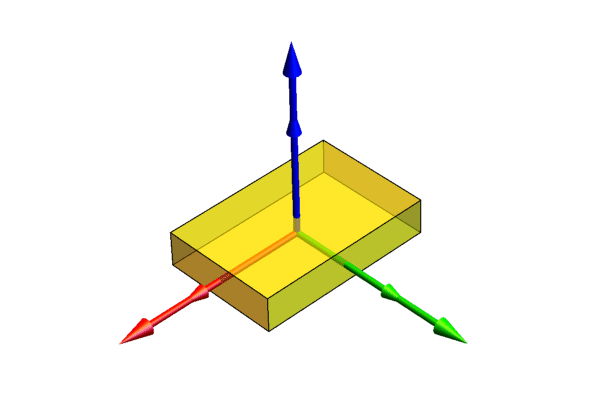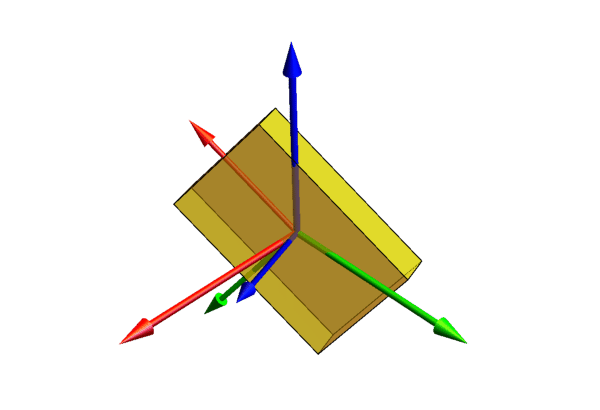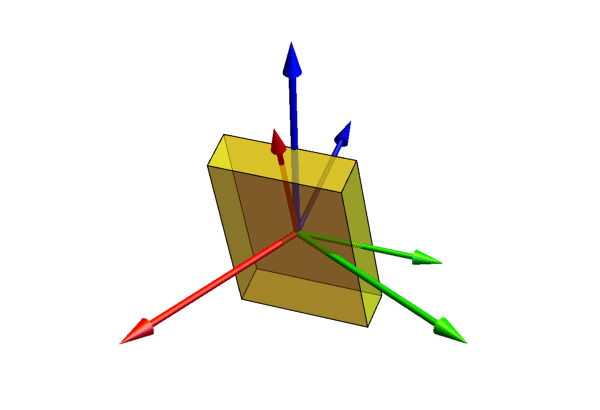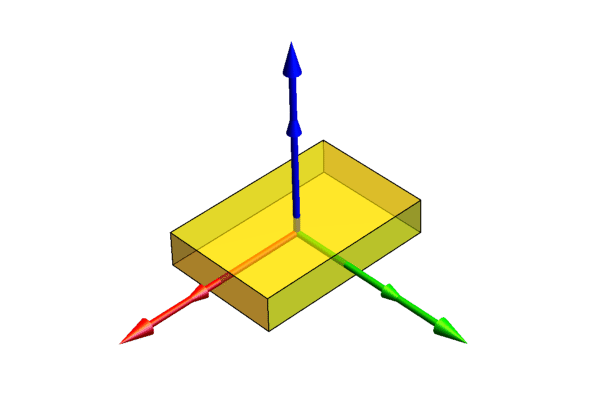
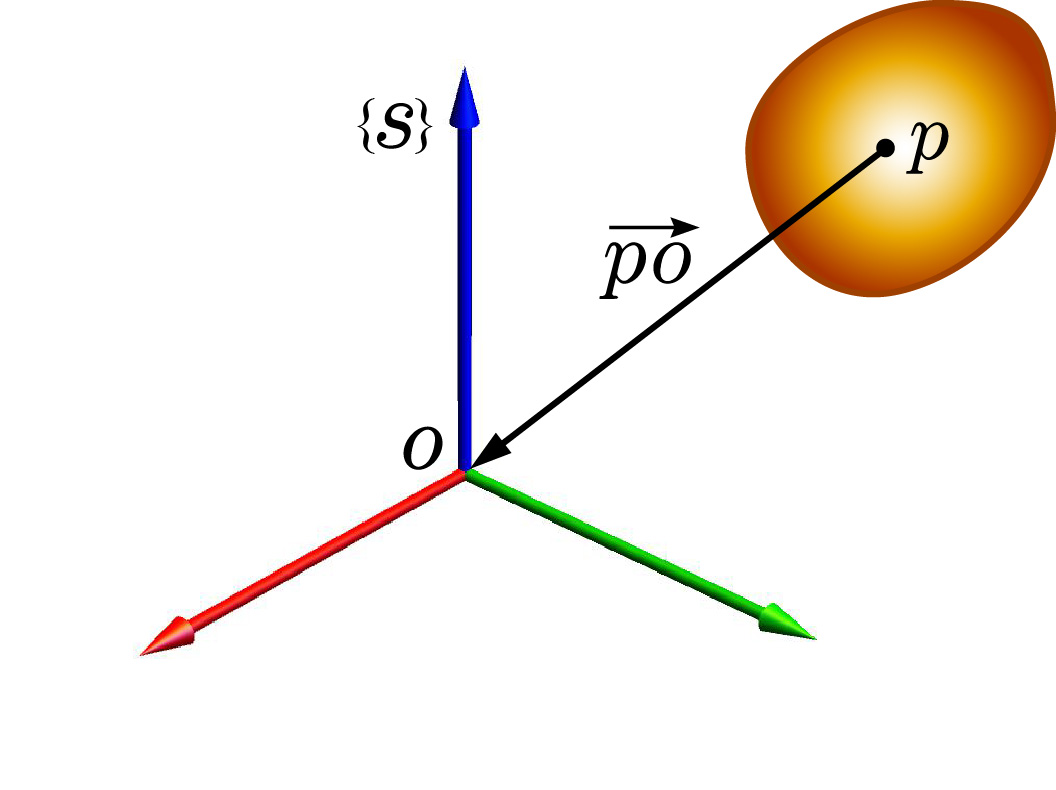
姿态应该怎么描述呢?如果在刚体 b上固定一个直角坐标系(记为 ${b}$),那么不管这个刚体怎么转动,它的姿态总是可以用与其固联的坐标系 ${b}$唯一描述的,如下图所示。(当然,位置和速度这些运动量都是相对的概念,要描述它们我们还需要一个参考坐标系,就是图中不动的那个,记为${s}$, ${s}$ 的原点记为 o。${b}$ 的原点记为 p ,p 在 ${s}$ 中的位置用向量 $\textbf{p}$ 表示)
直角坐标系 ${b}$ 可以用 $3\times3$ 的矩阵描述,这个矩阵被称为姿态矩阵,记为 $\textbf{R} $。姿态矩阵 $\textbf{R} $有一个性质:
$$\textbf{R}^{\rm{T}}\textbf{R}=\textbf{I}\tag{2} $$
这样,一个刚体的位置和姿态可以用 $\textbf{p}$ 和$\textbf{R}$ 完全描述。机器人学中最常用的方式是将位置和姿态捆绑起来,用一个矩阵一块表示,这个矩阵就是齐次变换矩阵,记为 $\textbf{g}$ :
$$\textbf{g}=\left[ \begin{matrix} \textbf{R} & \textbf{p}\ 0_{3\times1} & 1 \end{matrix} \right]\tag{3}$$
那么类比点的情况,刚体的速度是不是可以定义为矩阵 $\textbf{g}$ 的分量对时间的导数呢,如式 (4)所示?
$$\frac{d\textbf{g}}{dt}=\left[ \begin{matrix} \frac{d\textbf{R}}{dt} & \frac{d\textbf{p}}{dt}\ 0_{3\times1} & 0 \end{matrix} \right]\tag{4}$$
当然是可以的,不过还有更简洁的方法。别急,下面我一步步介绍怎么做。
空间速度——几何解释
在刚体 b 上有一个和它固定的点 p ,刚体运动时 p 点和它一起运动,如图下图所示。假如我们通过某种测量仪器知道了 p 点的速度$ v_{p}$ 和和刚体转动的角速度 $\omega$,那么我们该怎么描述刚体 b 的速度呢 ?(这里的 $v_{p}$ 和 $\omega$ 都是相对于参考坐标系$ {s}$ 的)
当然,用 $(v_{p}$,$\omega$) 就可以。但问题是 p 点只是我们随意选择的一个点,它并不比其它的点有更高的地位。我们暂时不讨论动力学,所以质心处的点也没有更高的地位。哪个点的地位不一样呢?既然刚体上的点地位都一样,我们把眼光瞄准了 o 点——参考坐标系的原点。可是等等, o 点不在刚体上啊?这里存在一个理解上的难点,我们可以这样想象,刚体 b 长胖了,胖到将 o 点也包括进去了。这时,刚体 b 上就有与 o 点瞬间重合的点。
利用理论力学中的基点法,我们就可以求出胖了的刚体与 o 重合的点的速度,即:
$$v_{o}=v_{p}+\omega\times\overrightarrow{po}\tag{5}$$
我们可以用 $(v_{o},\omega)$来描述刚体的速度。你可能会问,这么奇怪的表示方法有什么意义,下面我从另一种方式给出回答。
空间速度——代数解释
我们知道刚体的位置和姿态(合称位姿)可以用$\textbf{g}$ 描述,对于刚体上的任意一点r ,它相对于${s}$ 的位置用向量
$\textbf{r}$ 表示,那么在刚体运动后的位置是:
$$\left[ \begin{matrix} \textbf{r}\1 \end{matrix} \right]=\textbf{g}\left[ \begin{matrix} \textbf{r}\1 \end{matrix} \right]\tag{6}$$
对式 (6) 求导可得
$$\left[ \begin{matrix} \textbf{r}\1 \end{matrix} \right]=\dot{\textbf{g}}\left[ \begin{matrix} \textbf{r}\1 \end{matrix} \right]=\dot{\textbf{g}}\textbf{g}^{-1}\left[ \begin{matrix} \textbf{r}\1 \end{matrix} \right]\tag{7}$$
我们注意到出现了一个
$$\dot{\textbf{g}}\textbf{g}^{-1}=\left[ \begin{matrix} \dot{\textbf{R}} & \dot{\textbf{p}}\ 0_{3\times1} & 0 \end{matrix} \right]\left[ \begin{matrix} \textbf{R}^{-1} & -\textbf{R}^{-1}\textbf{p}\ 0_{3\times1} & 1 \end{matrix} \right]=\left[ \begin{matrix} \dot{\textbf{R}}\textbf{R}^{-1} & \dot{\textbf{p}}-\dot{\textbf{R}}\textbf{R}^{-1}\textbf{p}\ 0_{3\times1} & 0 \end{matrix} \right] \tag{8}$$
所以是空间速度(Spatial Velocity),这是第一个登场的速度。
$$\textbf{g}^{-1}\dot{\textbf{g}}=\left[ \begin{matrix} \textbf{R}^{-1} & -\textbf{R}^{-1}\textbf{p}\ 0_{3\times1} & 1 \end{matrix} \right]\left[ \begin{matrix} \dot{\textbf{R}} & \dot{\textbf{p}}\ 0_{3\times1} & 0 \end{matrix} \right]=\left[ \begin{matrix} \textbf{R}^{-1}\dot{\textbf{R}} & \textbf{R}^{-1}\dot{\textbf{p}}\ 0_{3\times1} & 0 \end{matrix} \right] \tag{9}$$
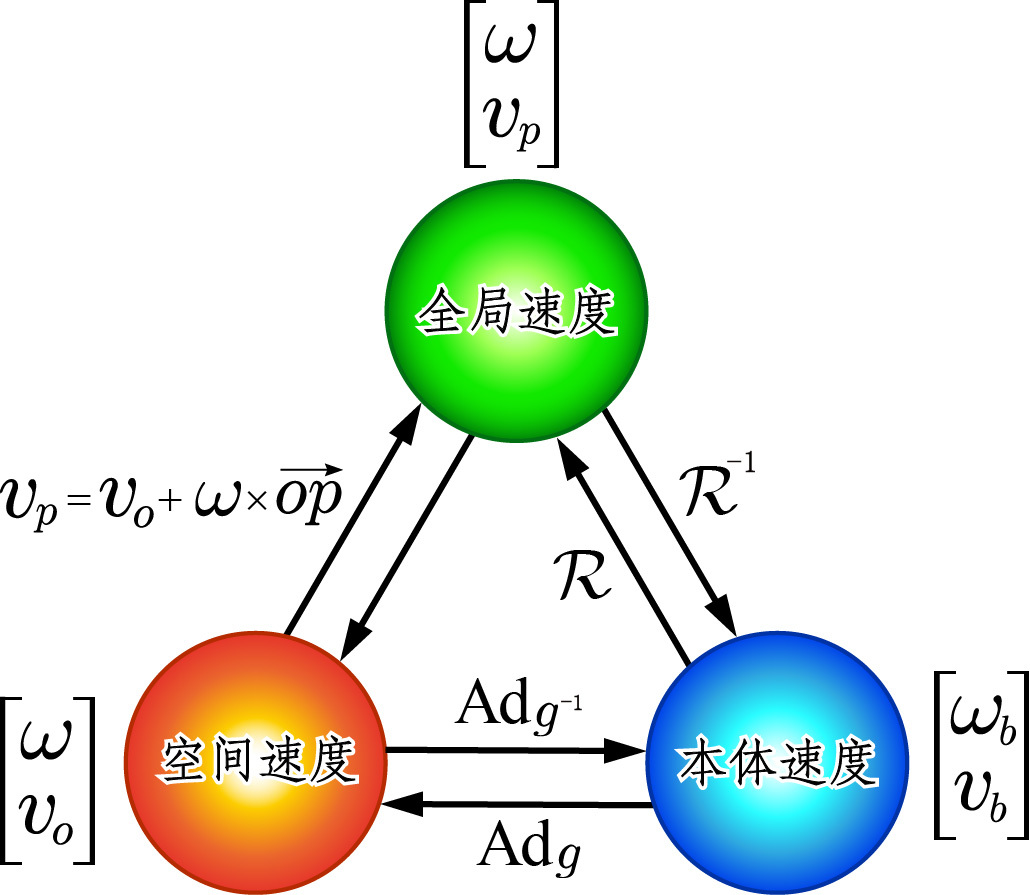
三个速度概念的变换方法如下图:
原文链接:https://blog.csdn.net/robinvista/article/details/69415962